This is a prelude to the post where I actually do computational modelling of point charge dynamics

After much thought about how to generalize the equation for electric field, I realized what was getting me stuck was my ignoring the $\hat{r}$ in the equation.

Now, substituting $\vec{\mathbb{r}} -\vec{\mathbb{x}}_\text{relative} $, we can “write down” a general electric field equation as a volume integral through the solid $\Omega$:

$\begin{align} \vec{\mathbf{E}}(\vec{\mathbf{r}}) &= {\displaystyle \int}_\mathbf{\Omega} k \frac{ \mathbb{e}(\vec{\mathbf{x}}) }{ \left| \vec{\mathbf{r}}-\vec{\mathbf{x}} \right| ^2 } \frac{ (\vec{\mathbf{r}}-\vec{\mathbf{x}}) }{ \left| \vec{\mathbf{r}}-\vec{\mathbf{x}} \right| } d\vec{\mathbf{x}} \\ &= {\displaystyle \int}_\mathbf{\Omega} k \frac{ \mathbb{e}(\vec{\mathbf{x}})(\vec{\mathbf{r}}-\vec{\mathbf{x}}) }{ \left| \vec{\mathbf{r}}-\vec{\mathbf{x}} \right| ^3 } d\vec{\mathbf{x}} \end{align}$ Where the integral is over a charged surface with surface charge density given by $\mathbb{e}(\vec{\mathbf{x}})$ . Now we can compute any electric field with this integral as our foundation. Any intuition we have, such as regarding symmetry can (1) be proven, and (2) used to simplify the integral, which will likely be very nasty depending on the complexity of the charge density function.

If we keep on exploring the equation, there are a number of places we can go. Firstly, we can solve the differential equation for the movement of n-particles in an arbitrary field, possibly with interparticle interaction. From an analytical standpoint, we can begin to characterize the different types of fields that can exist, i.e., the different stability classes.

Electric Fields and Neuroscience

I proclaim with excitement that fields are the most awesome concept I have ever encountered in all my education. I realized the language of field equations is the way to formally formulate an idea I had about neuronal computation. If we imagine the brain is actually a complex n-dimensional continuous surface approximated by the lattice network of neurons, then we can interpret the flow of neuronal firing frequencies as representing particles moving through the neuronal space. Then, we can start to think about what kind of field equations would govern neuronal particle dynamics. The particles and the field itself is dynamic and that is how learning happens. The same way real particles form physical structures embedded in the continuous “space lattice” as it were, neuronal particles that converge to a low energy part of the field can start to form structures in the interpreted continuous “brain space lattice”. Perhaps that is part of how learning happens.

Field Fitting

Before trying to develop such a theory, we can develop computational tools to “fit” a field to a dynamic/temporal dataset. If we have datapoints that move through a continuous n-dimensional space, we can imagine the space has a certain field governing how these datapoints flow. Then, we can ask the question – well, what is this field.

Some relevant links:

• Spin glasses
• Neural Networks and Vector Fields
• Mathematical Aspects of Spin Glasses
• Neural Networks and Statistical Learning

Basically, electric fields or action at a distance is about one of the coolest things around.

Examples

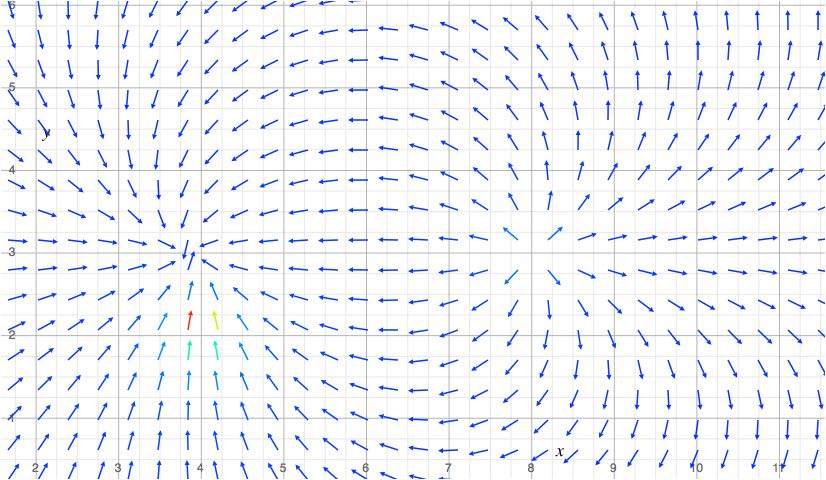
Dipole Field

The dipoles are $q_+ = (8,3)$ and $q_-=(4,2)$

$$\Delta \left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} \frac{\left( x-8 \right)3}{\left( 8-x \right)^{2}+\left( y-3 \right)^{2}}-\frac{\left( x-4 \right)5}{\left( 4-x \right)^{2}+\left( y-2 \right)^{2}} \\ \frac{\left( y-3 \right)3}{\left( 8-x \right)^{2}+\left( y-3 \right)^{2}}-\frac{\left( y-3 \right)5}{\left( 4-x \right)^{2}+\left( y-2 \right)^{2}} \end{array} \right]$$

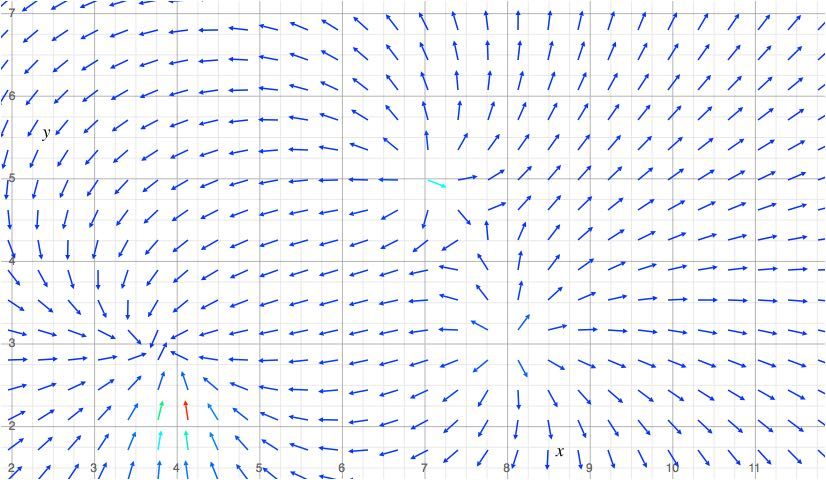
Tripole Fields

Basically just another term in the summation. I placed a positive charge $q_+=2$ at $(7, 5)$. We could go on forever doing this.

$$\Delta \left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} \frac{\left( x-8 \right)3}{\left( 8-x \right)^{2}+\left( y-3 \right)^{2}}-\frac{\left( x-4 \right)5}{\left( 4-x \right)^{2}+\left( y-2 \right)^{2}}+\frac{\left( x-7 \right)2}{\left( 7-x \right)^{2}+\left( y-5 \right)^{2}} \\ \frac{\left( y-3 \right)3}{\left( 8-x \right)^{2}+\left( y-3 \right)^{2}}-\frac{\left( y-3 \right)5}{\left( 4-x \right)^{2}+\left( y-2 \right)^{2}}+\frac{\left( y-5 \right)2}{\left( 7-x \right)^{2}+\left( y-5 \right)^{2}} \end{array} \right]$$

Why is this particularly interesting

Well we can compute electric fields to serve our computational needs. Let’s say we need to induce some action at a distance on an object. If we have the data, we can fit the a field to it, i.e. $q_i$ and $x_i$. Furthermore, we can simulate the dynamics of these fields.

Things get very interesting if we allow the point charges to move. How to analyze these dynamics is a very big question we need to answer. Also very computationally expensive?

Components of Electric Field on a Single Point

This is an example form of equation $(1)$ showing the contribution of each $(x,y)$ to the net eletcric field located at $(4,2)$. The charge function

$$\Delta \left[ \begin{array}{c} x \\ y \end{array} \right]=\left[ \begin{array}{c} \left( 4-x \right)\frac{\cos x}{\left( 4-x \right)^{2}+2^{2}} \\ \left( y \right)\frac{\cos x}{\left( 4-x \right)^{2}+2^{2}} \end{array} \right]$$

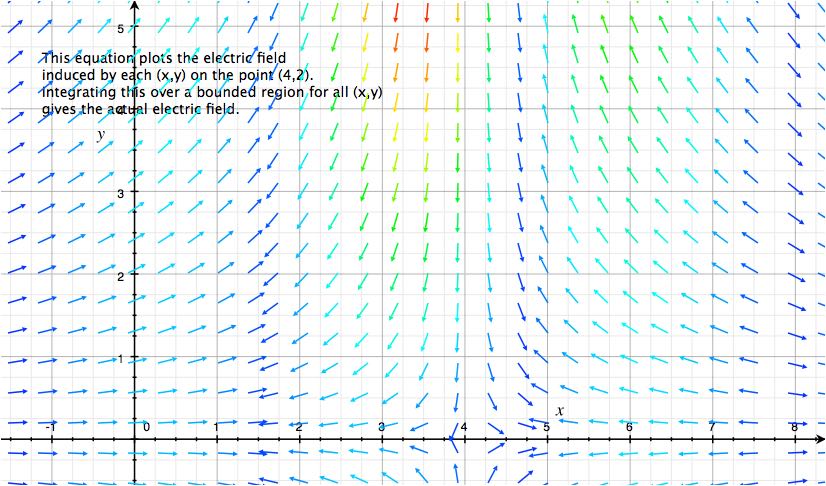
We have a function $Q$ and we are computing the field created by each $Q(\vec{x})$ on the single point $(4,0)$. Every single $x\in \mathbb{R^2}$ has such a field. Now, you can see how it gets incredibly computationally expensive to compute a net continuous field – we must do an extensive amount of combinatorial integration.

There Must be a Better Way

Yes there is. Gauss’s law. Coming up soon.