The following very nasty question came up in my physics homework this week:

Given two configurations, $C_1$, $C_2$ of $N$ point charges each determine the value of $N$ s.t. $U_1=U_2$.

$C_1$: $N$ point charges are uniformly distributed on a ring s.t. the distance between adjacent electrons is constant

$C_2$: $N-1$ point charges are uniformly distributed on a ring s.t. the distance between adjacent electrons is constant and one charge is placed in the center of the ring.

Crazy Solution

Let $N$ charges be arranged along a circle with radius $R$. The position of an arbitrary particle at an angle $\theta$ relative to the positive direction of the x-axis is $\vec{P}(\theta) = (R\cos\theta, R\sin\theta)$. Pick one charge located at angle $\theta = \theta_i$ and another particle located at $\theta = \theta_j$ relative to the positive direction of the x-axis. The distance between the two particles $\vec{r}$ is

$$\begin{aligned} \vec{r} & = \|\vec{P}(\theta_j) - \vec{P}(\theta_i)\| \\ & = \lVert(R\cos\theta_j, R\sin\theta_j) - (R\cos\theta_i, R\sin\theta_i)\rVert \\ & = R \sqrt{ \cos²\theta_j -2 \cos\theta_j\cos\theta_i + \cos²\theta_i + \sin²\theta_j -2 \sin\theta_j \sin\theta_i + \sin²\theta_i } \\ & = R\sqrt{ 1-\sin²\theta_j +1-\sin²\theta_i + \sin²\theta_j + \sin²\theta_i -2(\cos\theta_j\cos\theta_i+ \sin\theta_j \sin\theta_i) } \\ & = R\sqrt{ 2-2(\cos\theta_j \cos\theta_i + \sin\theta_j \sin\theta_i) }\\ & = R\sqrt{ 2-2(\cos(\theta_j-\theta_i)) } \\ & = R\sqrt{ 2-2(1-2\sin^2(\theta_j-\theta_i)) } \\ \therefore \vec{r} & = 2R\sin\left(\frac{\theta_j}{2}\right)\end{aligned}$$

Where

$$\begin{aligned} \theta_k &= k\Delta \theta \\ \Delta\theta &= \frac{2\pi}{N} \end{aligned}$$

We get

$$\begin{aligned} \vec{r} &=2R\sin\left(\frac{\theta_j}{2}\right) \\ & = 2R\sin\left(\frac{j2\pi}{2N}\right)\\ & = 2R\sin\left(\frac{j\pi}{N}\right)\\ \end{aligned}$$

With this expression for $\vec{r}$, we can write the net potential energy for particle $j$ along the circle with the equation assuming all particles have charges $q$

$$\begin{aligned} U_\text{particle i} & = \sum_{j=1}^{N-1} { \frac{q^2}{4\pi\epsilon_02R\sin\left(\frac{j\pi}{N}\right)}}\\ & = \frac{q^2}{8\pi\epsilon_0R}\sum_{j=1}^{N-1} {\csc\left(\frac{j\pi}{N}\right)} \end{aligned}$$

For concision, let

$$L = \frac{q^2}{8\pi\epsilon_0R}$$

Then net potential energy can be expressed as

$$\begin{aligned} U(n) = L\sum_{j=1}^{N-1}{\csc\left(\frac{j\pi}{n}\right)} \end{aligned}$$

For two configurations with $N$ charges we define the potential energies:

$$\begin{aligned} U_{N} &= \frac{N}{2}U(N) \\ U_{N-1} &= \frac{N-1}{2}U(N-1) + (N-1)2L \end{aligned}$$

where the second term in the definition of $U_2$ determines the potential for the lone particle in the center.

Now we solve for the $N$ at which $U_1 = U_2$

$$\begin{aligned} U_2-U_1 &= \Delta U \\ &= L\frac{N-1}{2}\sum_{j=1}^{N-2}{\csc\left(\frac{j\pi}{N-1}\right)} + L(N-1)2 - L\frac{N}{2}\sum_{j=1}^{N-1}{\csc\left(\frac{j\pi}{N}\right)} \\ &= L\left(\frac{N-1}{2}\sum_{j=1}^{N-2}{\csc\left(\frac{j\pi}{N-1}\right)} - \frac{N}{2}\sum_{j=1}^{N-1}{\csc\left(\frac{j\pi}{N}\right)} + 2(N-1) \right) \end{aligned}$$

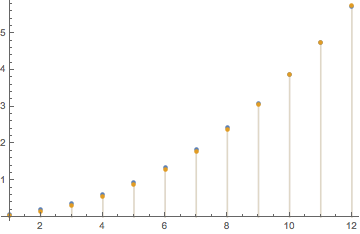
Which is really difficult to solve directly. But we can compute solutions:

  f[N_] = Sum[Csc[j*Pi/N], {j, 1, N - 1}]*1/(8*Pi)

DiscretePlot[{i/2*f[i] + i/(4*Pi), (i + 1)/2*f[i + 1]}, {i, 1, 12}]

And see the solution is for $N=12$